Page 114 - 《橡塑技术与装备》2023年5期
P. 114
橡塑技术与装备 CHINA RUBBER/PLASTICS TECHNOLOGY AND EQUIPMENT
减小 ;图 6(c),齿轮进入单齿啮合区,接触线总长 接触线总长度达到最小值,随后保持不变 ;图 8(d),
度达到最小值,随后保持不变 ;图 6(d),齿轮再次 齿轮再次进入双齿啮合区,接触线总长度逐渐增大,
进入双齿啮合区,接触线总长度逐渐增大,随后达到 随后达到图 8(a),齿轮完成一个啮合周期。
图 6(a),齿轮完成一个啮合周期。
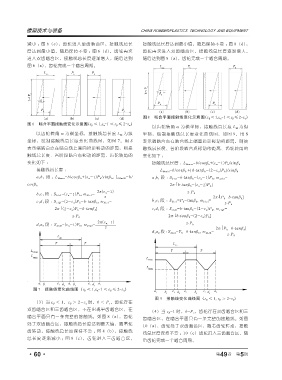
图 8 啮合平面接触线变化示意图(ε β < 1,ε α -1 < ε β ≤ 2-ε α )
图 6 啮合平面接触线变化示意图(ε β < 1,ε α -1 < ε β ≤ 2-ε α )
以齿轮转角 ω 为横坐标,接触线总长度 L M 为纵
以齿轮转角 ω 为横坐标,接触线总长度 L M 为纵 坐标,绘制接触线总长度变化曲线图,如图 9。用 S
坐标,绘制接触线总长度变化曲线图,如图 7。用 S 表示端啮合点在啮合线上端面投影移动的距离,则接
表示端啮合点在啮合线上端面投影移动的距离,则接 触线总长度、各阶段啮合点移动的距离、齿轮转角的
触线总长度、各阶段啮合点移动的距离、齿轮转角的 变化如下 :
变化如下 : 接触线总长度 : L Mmax =b/cosβ b +(ε α -1)P b /sinβ b
.
接触线总长度 : L Mmin =b/cosβ b +[b tanβ b -(2-ε α )P b ]/sinβ b
.
a 1 b 1 段: L Mmax =b/cosβ b +(ε α -1)P b /sinβ b , L MmIN =b/ a 1 b 1 段: S b1c1 =b tanβ b -(ε α -1)P b , ω a1b1 =
cosβ b 2π .[ b . tanβ b -(ε α -2)P b ]
b 1 c 1 段: S b1c1 =(ε α -1)P b , ω b1c1 = 2π(ε α -1) z . P b 2π .[ P b -b . tanβ b ]
z
.
c 1 d 1 段: S c1d1 =(2-ε α )P b -b tanβ b , ω b1c1 = b 1 c 1 段: S b1c1 =P b -tanβ b , ω b1c1 = z . P b
.
2π .[ (2-ε α )P b -b . tanβ b ] c 1 d 1 段: S c1d1 =b tanβ b -(2-ε α )P b , ω c1d1 =
z . P b 2π .[ b . tanβ b -(2-ε α )P b ]
d 1 a 2 段 : S d1d2 =(ε α -1)P b , ω d1a2 = 2π(ε α -1) z . P b
z 2π .[ P b -b . tanβ b ]
.
d 1 a 2 段: S d1a1 =P b -b tanβ b , ω d1a2 =
z . P b
图 7 接触线变化曲线图(ε β < 1,ε α -1 < ε β ≤ 2-ε α )
图 9 接触线变化曲线图(ε β < 1, ε β > 2-ε α )
(3)当 ε β < 1,ε β > 2-ε α 时,b < P z ,齿轮存在
双齿啮合区和三齿啮合区,不在出现单齿啮合区,在
(4)当 ε β =1 时,b=P z ,齿轮存在双齿啮合区和三
啮合平面只有一条完整的接触线。如图 8(a),齿轮
齿啮合区,在啮合平面只有一条完整的接触线。如图
处于双齿啮合区,接触线总长度达到最大值,随着轮
10(a),齿轮处于双齿啮合区,随着齿轮转动,接触
齿转动,接触线总长度保持不变 ;图 8(b),接触线
线总长度保持不变 ; 10(c)齿轮进入三齿啮合区,随
总长度逐渐减小 ;图 8(c),齿轮进入三齿啮合区,
后齿轮完成一个啮合周期。
5
·60· 第 49 卷 第 期