Page 92 - 《橡塑技术与装备》2023年10期

橡塑技术与装备 CHINA RUBBER/PLASTICS TECHNOLOGY AND EQUIPMENT

采用一个理想的交联网模型。对于一块各项同性的橡
胶试件，设取出其中之单位立方体，当发生了一般的
纯均匀应变后，立方体变为长方体如图 1 所示，同时
高分子链的末端也应发生相应的变化。
σ 3
I σ 2 λ
σ 1/√ λ
I 1 σ σ
σ 1
I 1/√ λ
σ
2 σ
3
（a）处于无应变状态；（b）处于均匀应变状态；（c）在单轴张力下
图 1 橡胶的单位立方体
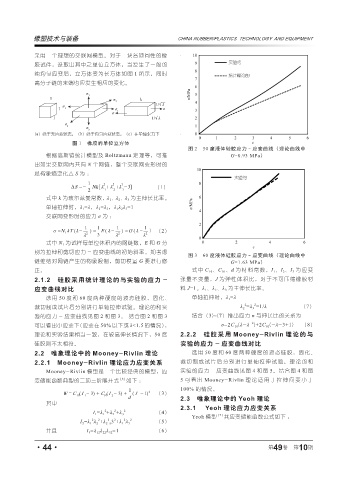
图 2 50 度液体硅胶应力 - 应变曲线（理论曲线中
根据高斯链统计模型及 Boltzmann 定理等，可推 G=0.93 MPa）
出如果交联网内共有 N 个网链，整个交联网变形时的
总构象熵变化△ S 为：
1 2 2 2
∆S = − 2 Nk [λ 1 + λ 2 +λ 3 − ] 3 （1）
式中 k 为玻尔兹曼常数，λ 1 、λ 2 、λ 3 为主伸长比率。
单轴拉伸时，λ 1 =λ，λ 2 =λ 3 ，λ 1 λ 2 λ 3 =1
交联网变形时的应力 σ 为：
1 1 1 1
σ =N 1 kT (λ − ) = E ( λ − ) =G (λ − ） （2）
λ 2 3 λ 2 λ 2
式中 N 1 为试样每单位体积内的网链数，E 和 G 分
别为拉伸和剪切应力 - 应变曲线的初始斜率。如考虑
图 3 60 度液体硅胶应力 - 应变曲线（理论曲线中
链缠结对网链产生的构象限制，剪切模量 G 要进行修 G=1.63 MPa）
正。 式中 C 10 、C 01 、d 为材料常数，I 1 、I 2 、I 3 为应变
2.1.2 硅胶采用统计理论的与实验的应力 - 张量不变量，J 为弹性体积比，对于不可压缩橡胶材
应变曲线对比 料 J=1。λ 1 、λ 2 、λ 3 为主伸长比率。

选用 50 度和 60 度两种硬度的液态硅胶，固化、 单轴拉伸时，λ 1 =λ
2
2
裁切制成试片后分别进行单轴拉伸试验。理论的和实 λ 2 =λ 3 =1/λ （7）
验的应力 - 应变曲线见图 2 和图 3。 结合图 2 和图 3 结合（3)~(7）推出应力 σ 与伸长比的关系为
-2
可以看出小应变下（应变在 50% 以下或 λ<1.5 的情况）， σ=2C 10 (λ-λ )+2C 01 (-λ-3+1) （8）
理论和实验结果相当一致，在较高伸长情况下，50 度 2.2.2 硅胶采用 Mooney-Rivlin 理论的与
硅胶则不太相符。 实验的应力 - 应变曲线对比
2.2 唯象理论中的 Mooney-Rivlin 理论 选用 50 度和 60 度两种硬度的液态硅胶，固化、
2.2.1 Mooney-Rivlin 理论应力应变关系 裁切制成试片后分别进行单轴拉伸试验。理论的和
Mooney-Rivlin 模型是一个比较经典的模型，应 实验的应力 - 应变曲线见图 4 和图 5。结合图 4 和图
变储能函数典型的二项三阶展开式 [6] 如下 ： 5 可看出 Mooney-Rivlin 理论适用于拉伸应变小于
1 100% 的情况。
2
W = C (I − ) 3 + C (I − ) 3 + ( J − ) 1 （3）
10
2
1
01
d 2.3 唯象理论中的 Yeoh 理论
其中
2.3.1 Yeoh 理论应力应变关系
2
2
2
I 1 =λ 1 +λ 2 +λ 3 （4） [7]
Yeoh 模型 其应变储能函数公式如下 ：
2 2 2 2 2 2
I 2 =λ 1 λ 2 +λ 2 λ 3 +λ 1 λ 3 （5）
并且 I 3 =λ 12 λ 22 λ 32 =1 （6）
·44· 第 49 卷 第 10 期